Murphet vs Prophet — When Beta Beats Gaussian

Head-to-Head Comparison

Feature	Prophet	Murphet	Advantage
Likelihood	Gaussian / Student-t	Beta (0-1) or Student-t	✓ Murphet
Valid bounds	Manual logistic "cap"	Built-in logit link function	✓ Murphet
Changepoints	Hard, piece-wise linear	Smooth logistic transitions	✓ Murphet
Residual structure	Assumes independence	Optional AR(1) disturbance	✓ Murphet
Heteroscedasticity	None	Automatic adaptation	✓ Murphet
Heavy tails	Student-t noise only	Student-t or β-head with φ-scaling	✓ Murphet
Holidays & events	Built-in support	Use changepoints (planned for future)	~ Prophet
Maturity	Established ecosystem	Newer, focused implementation	~ Prophet

When To Use Murphet

📊

Rate & Proportion Data

Murphet excels with any data naturally bounded between 0 and 1: churn rates, conversion rates, occupancy levels, adoption percentages, and market share metrics.

📈

E-commerce Metrics

Click-through rates, add-to-cart rates, checkout conversion, and other e-commerce KPIs that must stay within valid bounds benefit from Murphet's Beta likelihood.

🏨

Accommodation & Travel

Hotel occupancy forecasting, flight load factors, and rental capacity utilization rates show dramatic accuracy improvements with Murphet's bounded predictions.

🏬

Retail Operations

Inventory-to-sales ratios, product return rates, and discount penetration rates maintain realistic bounds even in volatile market conditions.

📱

Product Analytics

User retention, feature adoption rates, and engagement metrics benefit from Murphet's smooth changepoints during product launches and updates.

🔮

Seasonal Business KPIs

Business metrics with strong seasonal patterns and strict physical bounds (like utilization percentages) benefit from Murphet's enhanced seasonal modeling.

When to Stick with Prophet

While Murphet outperforms Prophet for bounded metrics, there are cases where Prophet remains a better choice:

Unbounded forecasts where logistic constraints aren't appropriate
Holiday-heavy series requiring Prophet's built-in holiday modeling
Count data that would be better served by Poisson/negative binomial models

Extremely large datasets where Prophet's C++ backend outperforms Stan
Established workflows heavily integrated with Prophet's exact API
Ultra-long forecasts where boundary constraints are less critical

Murphet's Technical Edge

Why Beta Beats Gaussian

For bounded metrics like rates and proportions, Murphet's Beta likelihood provides three critical advantages:

Intrinsic bounds preservation

The Beta distribution is naturally bounded between 0 and 1, ensuring predictions never cross impossible thresholds.
Heteroscedastic uncertainty

Variance naturally decreases near boundaries, creating more realistic prediction intervals that respect physical constraints.
Shape flexibility

Beta can model skewed distributions, unlike Gaussian models that assume symmetry around the mean.

# Prophet requires manual "cap" to bound predictions
    prophet_df = df.copy()
    prophet_df['cap'] = 1.0  # Manual upper bound
    prophet_model = Prophet(growth='linear', mcmc_samples=0)
    prophet_model.fit(prophet_df)

    # Murphet naturally respects bounds with Beta likelihood
    murphet_model = fit_churn_model(
        t=df['t'],
        y=df['y'],
        likelihood="beta",  # Automatically ensures 0 < predictions < 1
        periods=12,
        num_harmonics=3
    )

Smooth Transitions & Persistent Patterns

Prophet's Sharp Changepoints:

Prophet uses hard changepoints that create unrealistic kinks in forecasts. The model is also memoryless—each residual is independent of previous observations.

f(t) = k·t + m + Σ δⱼ·I(t > sⱼ)·(t - sⱼ)

Where I() is an indicator function causing abrupt slope changes

Murphet's Improvements:

Murphet implements smooth logistic transitions between trend segments and captures autocorrelation with an AR(1) component:

f(t) = k·t + m + Σ δⱼ·σ(γ·(t - sⱼ))·(t - sⱼ) + AR(1)

Where σ() is the sigmoid function for smooth transitions and AR(1) captures pattern persistence

Real-world Impact:

More natural-looking forecasts without artificial kinks
Better adaptation to gradual market shifts
Improved capture of persistent deviations through economic cycles
Reduced forecast volatility during trend transitions

Performance Benchmarks

In rigorous Optuna-tuned cross-validation studies, Murphet consistently outperforms Prophet for bounded metrics.

Hotel Occupancy (High Tariff A)

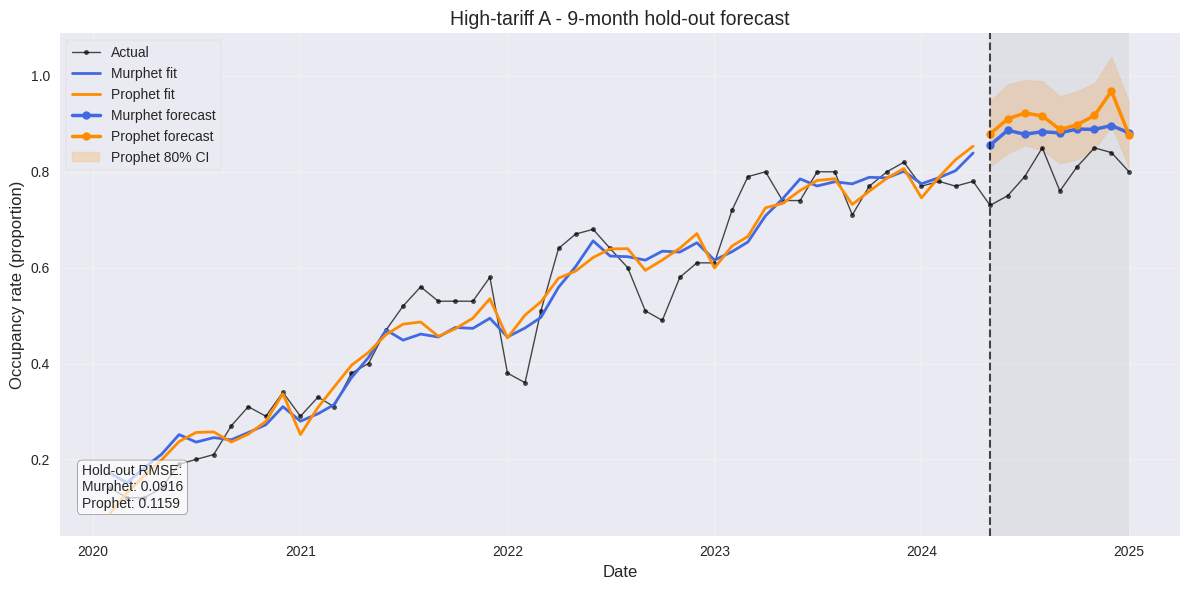
9-month hold-out test:

Murphet RMSE: 0.091 | Prophet RMSE: 0.158

42% error reduction

Retail Inventories-to-Sales Ratio

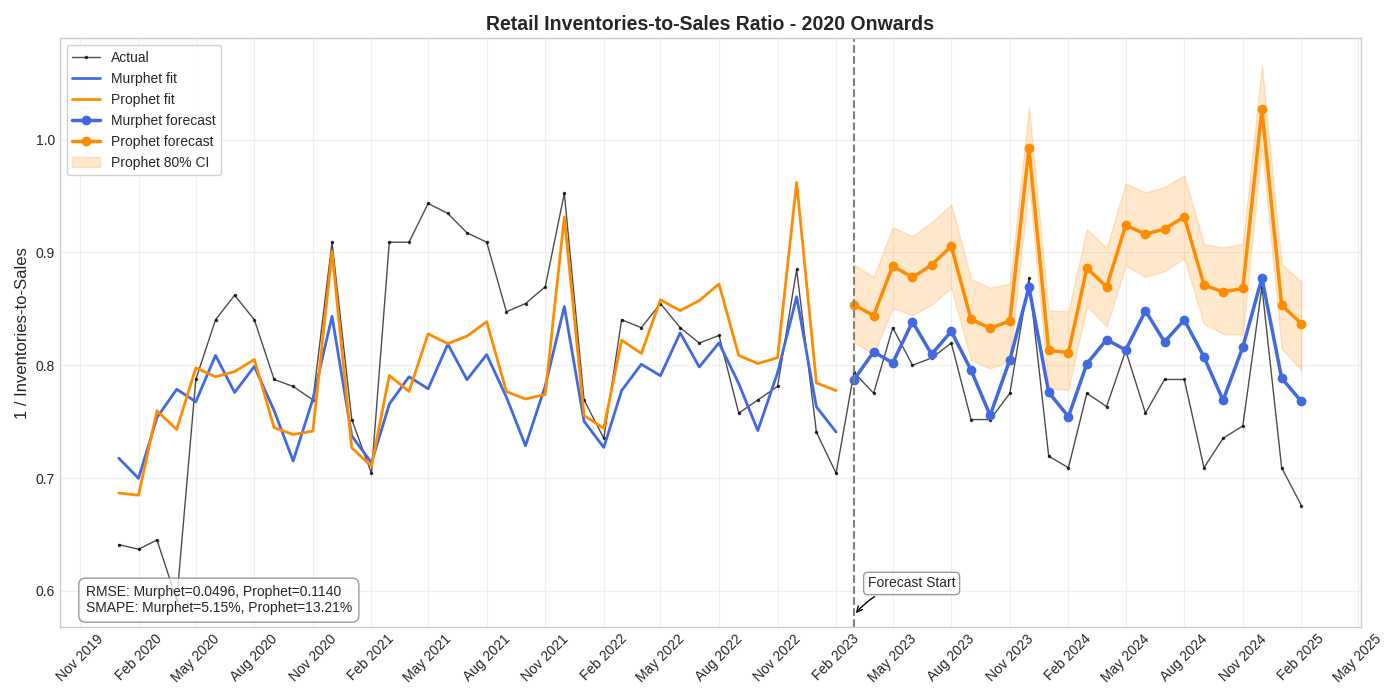
Retail inventory-to-sales ratio forecast comparison

12-month hold-out test:

Murphet RMSE: 0.050 | Prophet RMSE: 0.114

56% error reduction

Residual Analysis

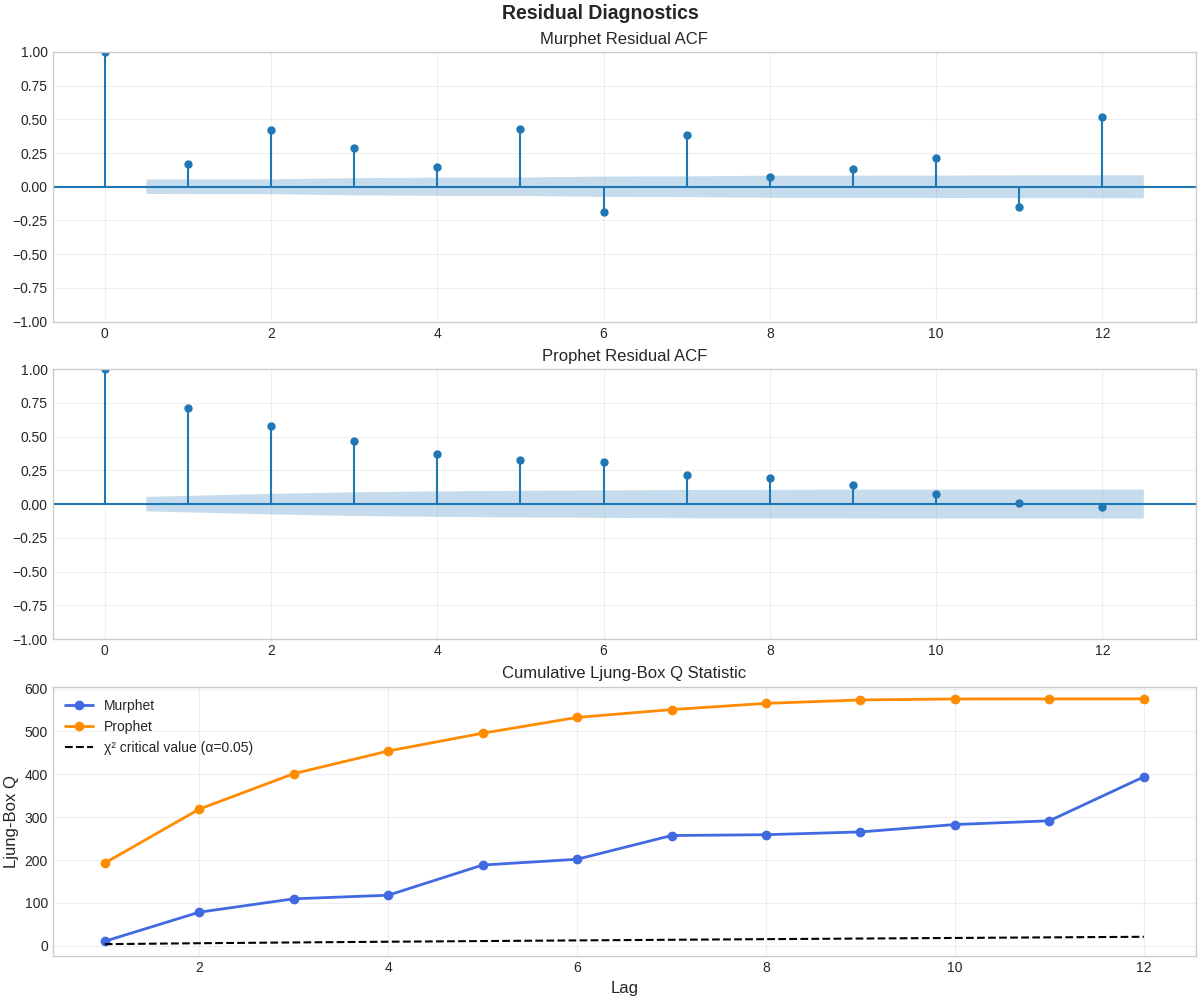
Murphet's residuals show significantly lower autocorrelation and reduced Ljung-Box Q statistics, indicating better capture of underlying patterns and more reliable predictions.

Migrating from Prophet to Murphet

If you're already using Prophet for forecasting rates or proportions, transitioning to Murphet is straightforward:

# --- Prophet code ---
    from prophet import Prophet
    m = Prophet(
        changepoint_prior_scale=0.05,
        seasonality_prior_scale=10.0,
        seasonality_mode='additive',
        mcmc_samples=0
    )
    m.fit(df)
    future = m.make_future_dataframe(periods=12)
    forecast = m.predict(future)

    # --- Equivalent Murphet code ---
    from murphet import fit_churn_model
    model = fit_churn_model(
        t=df['t'],                 # Numeric index
        y=df['y'],                 # Target values (between 0-1)
        likelihood="beta",         # For bounded metrics
        delta_scale=0.05,          # Same as changepoint_prior_scale
        season_scale=1.0,          # Similar to seasonality_prior_scale/10
        periods=12.0,              # Yearly seasonality
        num_harmonics=3,           # Complexity of seasonal pattern
        inference="map"            # Fast point estimates (like mcmc_samples=0)
    )
    future_t = np.arange(df['t'].iloc[-1] + 1, df['t'].iloc[-1] + 13)
    forecast = model.predict(future_t)

The Right Tool for Bounded Forecasts

"Prophet is an excellent general-purpose forecasting tool. Murphet is the specialist when your data has natural bounds."

Murphet isn't meant to replace Prophet in every scenario—it's designed to excel in the specific domain of rate and proportion forecasting where physical constraints matter.

Get Started GitHub