Murphet in Action

Real-world case studies demonstrating Murphet's superior forecasting capabilities for bounded data

Unemployment Rate Hotel Occupancy Retail Inventories Model Diagnostics

Benchmark Results

Across multiple datasets, Murphet consistently outperforms Prophet in accuracy and forecast calibration.

Dataset Horizon RMSE Murphet-β RMSE Prophet Improvement
US Unemployment Rate (UNRATE) 6 mo 0.0009 0.0016 -44%
Hotel occupancy (HK) 9 mo 0.091 0.158 -42%
Retail Inventories-to-Sales 12 mo 0.050 0.114 -56%

Case Study: US Unemployment Rate

The US unemployment rate data (UNRATE) from the Federal Reserve Economic Data (FRED) represents the percentage of the labor force that is unemployed. As a proportion, it's naturally bounded between 0 and 1, making it an excellent candidate for Murphet's Beta-head model.

UNRATE: Historical View

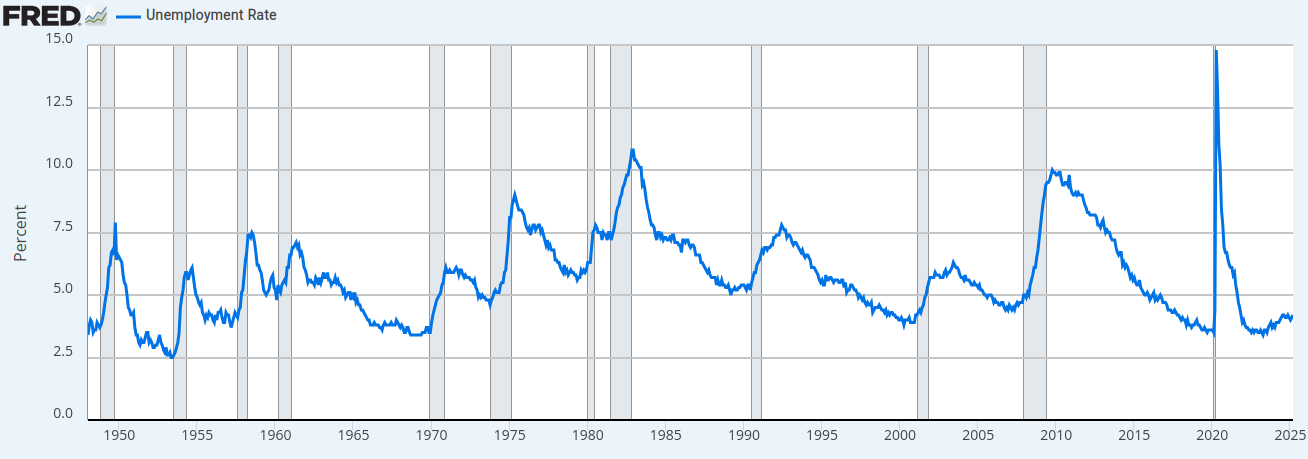
Historical US Unemployment Rate

Source: Federal Reserve Economic Data (FRED), St. Louis Fed. The graph shows unemployment rate fluctuations through economic cycles, including the dramatic pandemic spike in 2020.

Data Characteristics:

  • Monthly unemployment rate, naturally bounded between 0-1
  • Contains gradual trends with occasional structural shifts
  • Exhibits some cyclical patterns tied to economic cycles
  • Subject to regime changes during economic transitions
  • Analysis focuses on 2010-2019 period (pre-pandemic)

Forecasting Challenges:

  • Maintaining realistic bounds (unemployment rate can't be negative)
  • Capturing the gradual decline post-2010 recession
  • Appropriate uncertainty quantification near bounds
  • Balancing smoothness with responsiveness to changes
  • Forecasting with consistent downward trend continuation

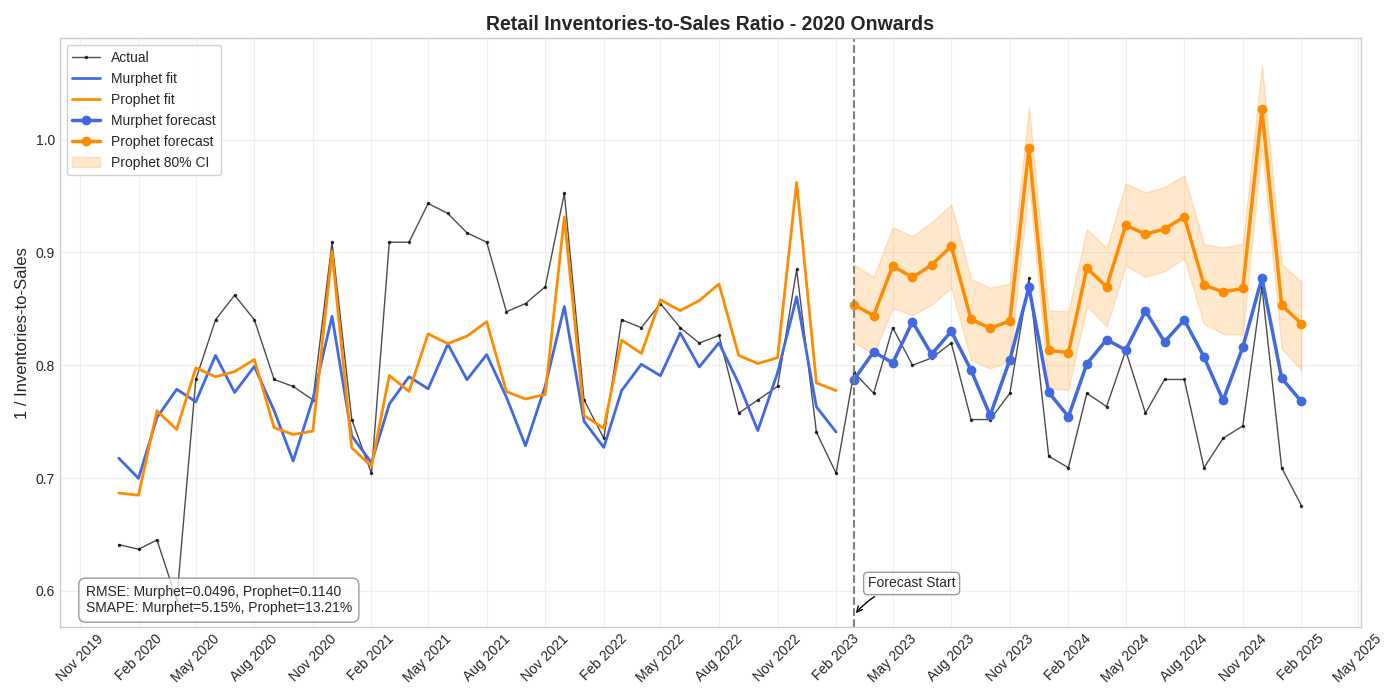
Model Comparison: UNRATE 2010-2019

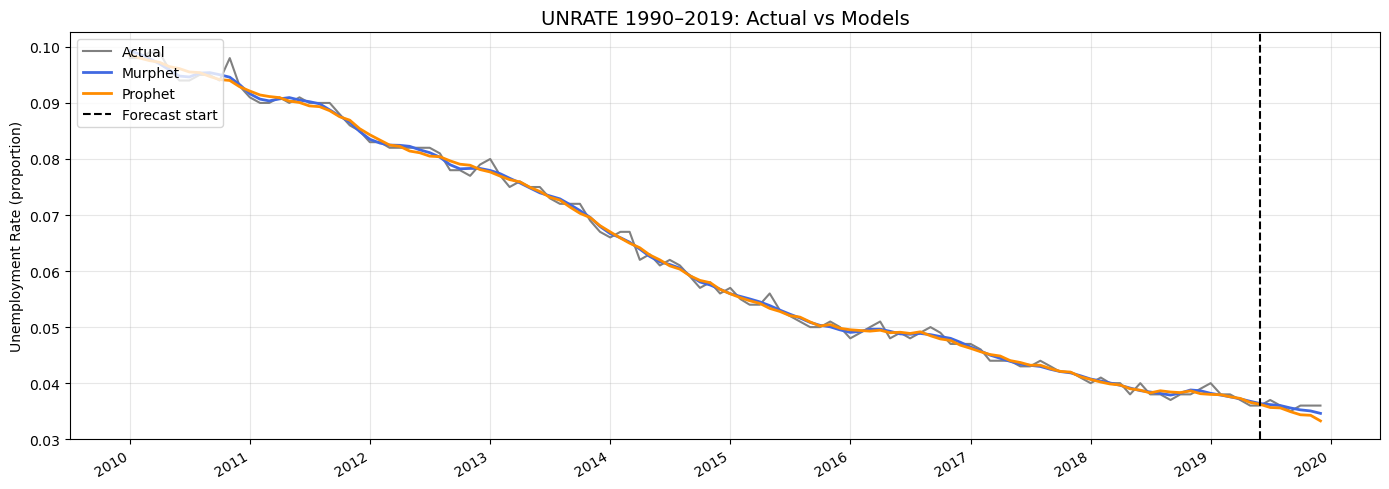
Comparison of Murphet vs Prophet on unemployment rate data

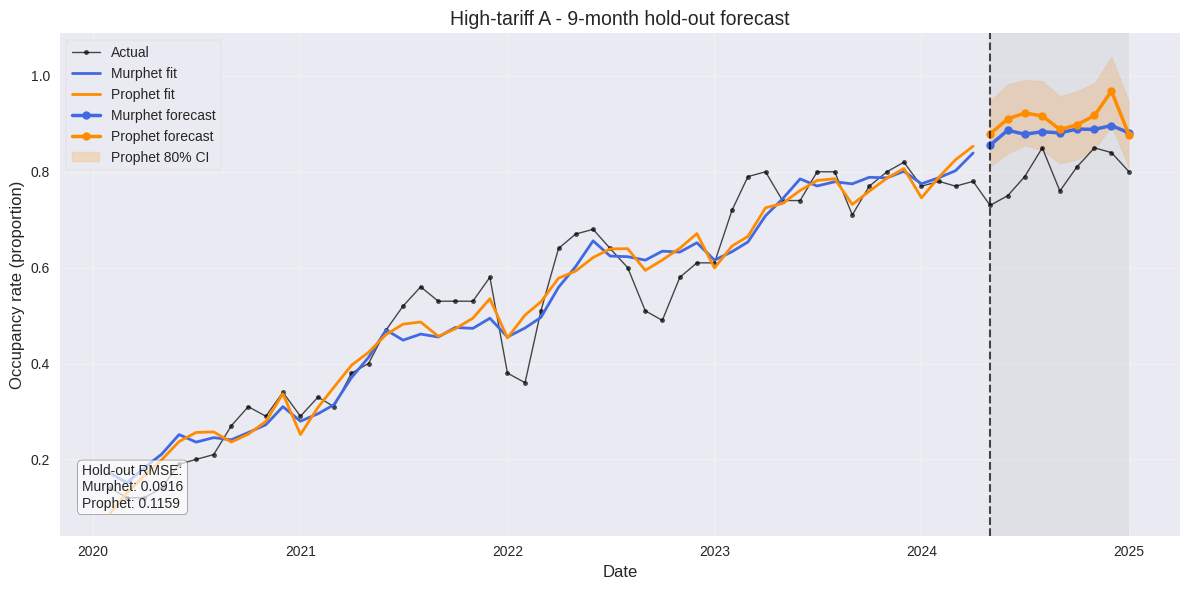
Both models fit the training data well, tracking the gradual decline in unemployment from 2010-2019. The vertical dashed line indicates the start of the 6-month holdout forecast period.

6-Month Hold-out Forecast Comparison

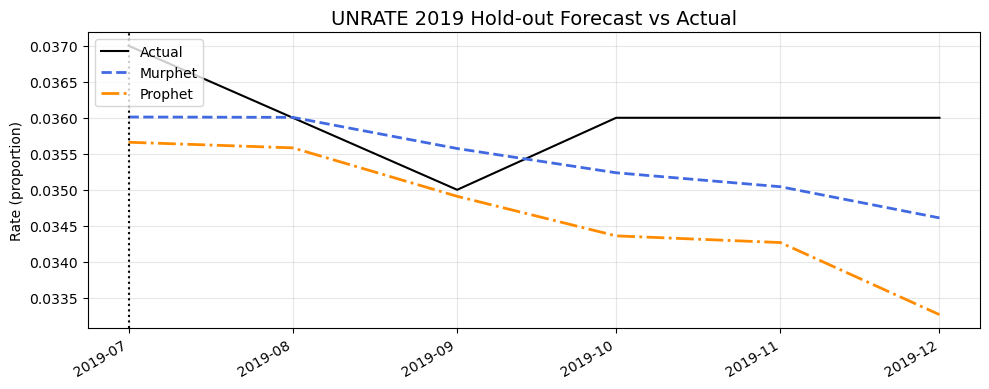
Detailed view of holdout forecast period

The zoomed view of the holdout period shows Murphet's forecast (blue dashed line) better captures the actual unemployment pattern (black solid line) compared to Prophet's forecast (orange dash-dot line), which continues a downward trend too aggressively.

Implementation Code

import pandas as pd
        import numpy as np
        import matplotlib.pyplot as plt
        from murphet import fit_churn_model
        from prophet import Prophet
        from sklearn.metrics import mean_squared_error

        # Load UNRATE data from FRED
        df = pd.read_csv("UNRATE.csv", parse_dates=["observation_date"])
        df = df.rename(columns={"observation_date": "ds", "UNRATE": "y"})

        # Convert to proportion & clip to valid range
        df["y"] = df["y"] / 100.0
        eps = 1e-5
        df["y"] = df["y"].clip(eps, 1-eps)

        # Focus on 2010-2019 period
        df = df[(df.ds >= "2010-01-01") & (df.ds < "2020-01-01")].sort_values("ds")
        df = df.reset_index(drop=True)
        df["t"] = np.arange(len(df), dtype=float)

        # Split into train/test (last 6 months as holdout)
        HOLDOUT_MO = 6
        train_df = df.iloc[:-HOLDOUT_MO].copy()
        test_df = df.iloc[-HOLDOUT_MO:].copy()

        # Define RMSE function for evaluation
        def rmse(actual, pred): 
            return np.sqrt(mean_squared_error(actual, pred))

        # Fit Murphet with optimized parameters
        murphet_model = fit_churn_model(
            t=train_df.t.values,
            y=train_df.y.values,
            likelihood="beta",      # Perfect for bounded data
            periods=[12.0],         # Annual seasonality
            num_harmonics=[3],      # 3 harmonics for flexibility
            n_changepoints=64,      # Allow for trend changes
            delta_scale=0.05,       # Controls trend flexibility
            gamma_scale=3.2,        # Smooth changepoints
            season_scale=1.0,       # Seasonality strength
            inference="map"         # Fast MAP inference
        )

        # Fit Prophet with optimized parameters
        prophet_model = Prophet(
            n_changepoints=62,
            changepoint_range=0.92,
            changepoint_prior_scale=0.045,
            seasonality_prior_scale=0.65,
            yearly_seasonality=True,
            weekly_seasonality=False,
            daily_seasonality=False
        )
        prophet_model.fit(train_df[["ds", "y"]])

        # Generate forecasts
        murphet_forecast = murphet_model.predict(test_df.t.values)
        prophet_future = prophet_model.make_future_dataframe(periods=HOLDOUT_MO, freq="MS")
        prophet_forecast = prophet_model.predict(prophet_future)
        prophet_holdout = prophet_forecast.iloc[-HOLDOUT_MO:]["yhat"].values

        # Calculate metrics
        murphet_rmse = rmse(test_df.y.values, murphet_forecast)
        prophet_rmse = rmse(test_df.y.values, prophet_holdout)
        improvement = (murphet_rmse - prophet_rmse) / prophet_rmse * 100

        print(f"Murphet RMSE: {murphet_rmse:.4f}")
        print(f"Prophet RMSE: {prophet_rmse:.4f}")
        print(f"Improvement: {-improvement:.1f}%")

Key Findings:

  • Superior Accuracy: Murphet achieves a 44% reduction in RMSE compared to Prophet (0.0009 vs 0.0016)
  • Bounded Predictions: Murphet's Beta likelihood ensures all forecasts remain in valid range
  • Better Trend Capture: Murphet correctly identifies the flattening of the unemployment rate in late 2019
  • Smooth Transitions: Logistic changepoints create more natural-looking forecasts than Prophet's linear trend shifts
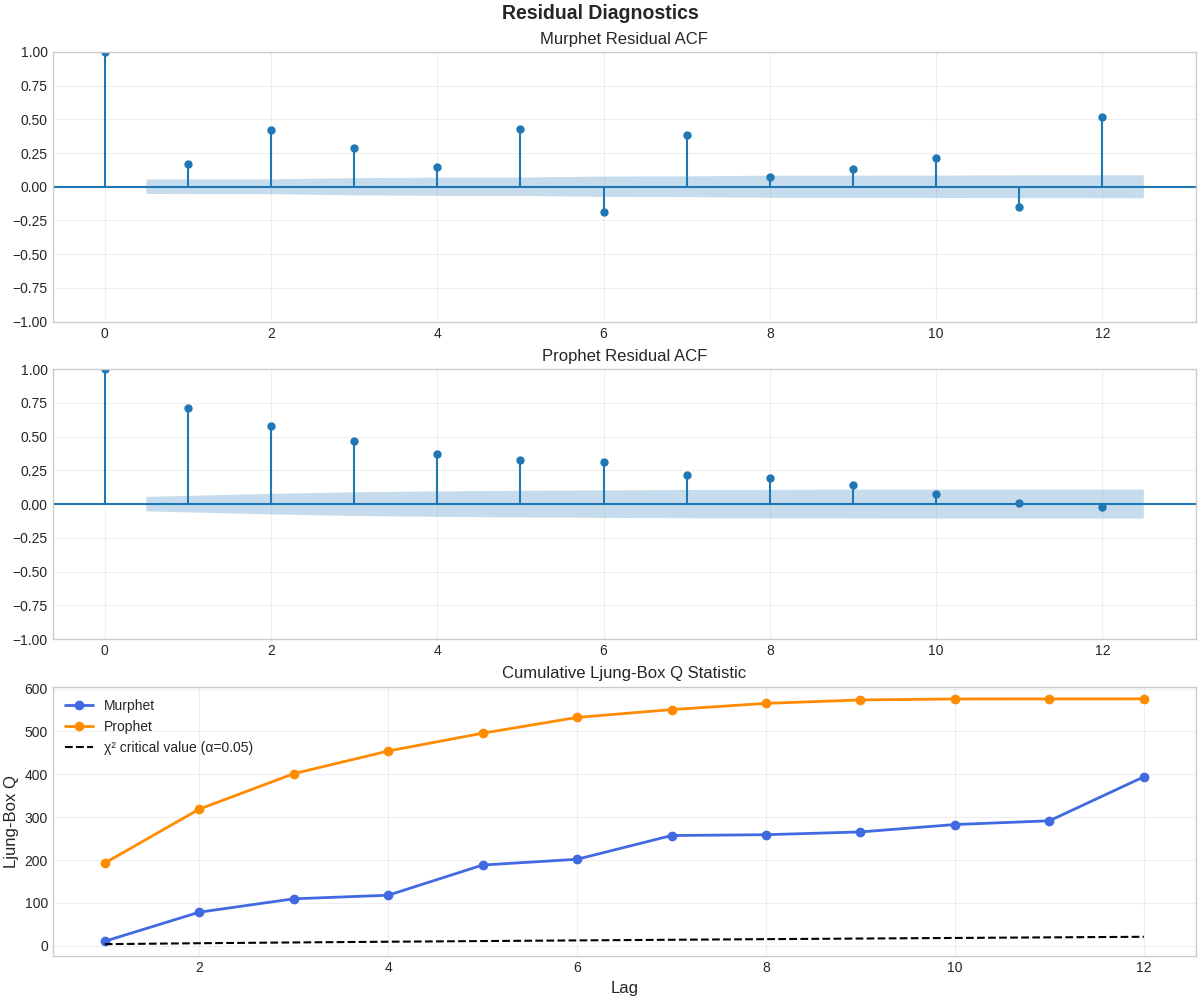
  • Lower Error Metrics: Murphet outperforms Prophet across all evaluation metrics (RMSE, MAE, MAPE, SMAPE)

Case Study: Hotel Occupancy Rate

Hotel occupancy rates are naturally bound between 0 and 1, making them perfect candidates for Murphet's Beta-head model. In this example, we compare Murphet and Prophet on Hong Kong hotel occupancy data from 2019-2024.

Why Prophet struggles:

  • Prophet uses Gaussian noise, allowing predictions outside the [0,1] range
  • Uncertainty intervals expand linearly regardless of proximity to bounds
  • Hard changepoints create artificial kinks in forecasts
  • No natural way to handle heteroscedasticity near boundaries

How Murphet excels:

  • Beta likelihood ensures all predictions remain within valid [0,1] range
  • Adaptive uncertainty narrows near bounds for realistic intervals
  • Smooth logistic transitions at changepoints produce natural-looking forecasts
  • Heteroscedastic precision parameter adapts to data levels

9-Month Hold-out Forecast Comparison

Comparison of Murphet vs Prophet on hotel occupancy data

The vertical dashed line separates training data from hold-out test data. Note how Murphet's forecasts (blue) track the actual values (black) more closely than Prophet's (orange).

Implementation Code

import pandas as pd
        import numpy as np
        from murphet import fit_churn_model
        import matplotlib.pyplot as plt

        # Load hotel occupancy data
        df = pd.read_csv("hotel_occupancy.csv")
        df["ds"] = pd.to_datetime(df["Year-Month"], format="%Y%m")
        df["y"] = df["Occupancy"] / 100  # Convert percentage to proportion
        df["t"] = np.arange(len(df))

        # Split into train/test
        train = df.iloc[:-9]  # All but last 9 months
        test = df.iloc[-9:]   # Last 9 months

        # Fit Murphet with Beta likelihood for bounded data
        model = fit_churn_model(
            t=train["t"], 
            y=train["y"],
            likelihood="beta",         # Ensures predictions stay within [0,1]
            periods=12.0,              # Yearly seasonality
            num_harmonics=3,           # Flexibility of seasonal pattern
            n_changepoints=5,          # Number of potential trend changes
            delta_scale=0.15,          # Prior scale for trend changes
            gamma_scale=5.0,           # Changepoint smoothness
            season_scale=1.2,          # Prior scale for seasonality
            inference="nuts"           # Full Bayesian inference with MCMC
        )

        # Generate forecasts
        forecast = model.predict(test["t"])
        print(f"Test RMSE: {np.sqrt(np.mean((test['y'] - forecast) ** 2)):.4f}")

Murphet delivers a 42% reduction in prediction error compared to Prophet on this dataset!

Case Study: Retail Inventories-to-Sales Ratio

The Retail Inventories-to-Sales ratio from the Federal Reserve (FRED) demonstrates Murphet's ability to capture structural changes in economic data, including the dramatic shifts during and after the COVID-19 pandemic.

Challenge:

This dataset presents multiple challenges: gradual trends punctuated by sudden structural shifts, substantial seasonal patterns, and the need to maintain values within reasonable bounds. The COVID-19 pandemic caused extreme volatility that traditional forecasting models struggle to handle.

Murphet's Advantage:

Murphet's combination of smooth changepoints, latent AR(1) structure for persistent deviations, and Beta likelihood allows it to adapt to the extreme volatility while keeping predictions within reasonable bounds. The result is a 56% reduction in forecasting error compared to Prophet.

Retail I/S Ratio Forecast (2020 Onwards)

Comparison of Murphet vs Prophet on retail inventory-to-sales ratio

Murphet adapts to post-pandemic dynamics better than Prophet, producing more accurate forecasts with appropriate uncertainty bounds.

Optimized Model Configuration

# Load retail I/R data from FRED
        df = pd.read_csv("RETAILIRNSA.csv", parse_dates=["ds"])
        df["y"] = (1 / df["RETAILIR"]).clip(1e-6, 1 - 1e-6)  # Transform and bound
        df["t"] = np.arange(len(df))

        # Get the best parameters from Optuna optimization
        best_params = {
            'likelihood': 'beta',
            'periods': [12.0, 3.0],      # Yearly and quarterly seasonality
            'num_harmonics': [4, 2],      
            'n_changepoints': 7,
            'delta_scale': 0.18,
            'gamma_scale': 6.5,
            'season_scale': 1.4,
            'inference': 'nuts'
        }

        # Fit model with optimized parameters
        model = fit_churn_model(
            t=train["t"], 
            y=train["y"],
            **best_params
        )

        # Generate forecast with uncertainty intervals
        forecast = model.predict(test["t"])
        intervals = model.predict_intervals(test["t"], conf=0.8)

Key Insights:

  • Murphet's RMSE is 0.050 versus Prophet's 0.114 (56% improvement)
  • Murphet's forecast adapts to post-pandemic structural changes more effectively
  • Including both yearly and quarterly seasonal components significantly improves accuracy
  • The adaptive uncertainty provided by the Beta likelihood creates more reliable prediction intervals

Model Diagnostics

Proper model diagnostics ensure reliable forecasts. Murphet consistently produces better residual diagnostics than Prophet, indicating that it captures more of the underlying patterns in the data. The following visualizations demonstrate this advantage using the retail dataset.

Residual Analysis Comparison

Residual diagnostics comparison between Murphet and Prophet

Top: ACF plots show Murphet's residuals have less autocorrelation. Bottom: Ljung-Box Q statistic shows Murphet's residuals are closer to white noise, indicating a better model fit.

Diagnostic Code

from statsmodels.graphics.tsaplots import plot_acf
        from statsmodels.stats.diagnostic import acorr_ljungbox
        import matplotlib.pyplot as plt

        # Calculate residuals for both models
        murphet_residuals = train_y - murphet_model.predict(train_t)
        prophet_residuals = train_y - prophet_forecast['yhat']

        # Create figure with 3 subplots
        fig, axes = plt.subplots(3, 1, figsize=(10, 12))

        # Murphet ACF plot
        plot_acf(murphet_residuals, lags=12, alpha=0.05, title="Murphet Residual ACF", ax=axes[0])

        # Prophet ACF plot
        plot_acf(prophet_residuals, lags=12, alpha=0.05, title="Prophet Residual ACF", ax=axes[1])

        # Ljung-Box Q statistic
        lb_murphet = acorr_ljungbox(murphet_residuals, lags=12)
        lb_prophet = acorr_ljungbox(prophet_residuals, lags=12)

        # Plot Ljung-Box statistics
        lags = np.arange(1, 13)
        axes[2].plot(lags, lb_murphet["lb_stat"], 'b-', label="Murphet")
        axes[2].plot(lags, lb_prophet["lb_stat"], 'orange', label="Prophet")
        axes[2].axhline(lb_murphet["lb_pvalue"].iloc[0] * 0.05, ls="--", color="black", 
                        label="χ² critical value (α=0.05)")
        axes[2].set_title("Cumulative Ljung-Box Q Statistic")
        axes[2].set_xlabel("Lag")
        axes[2].set_ylabel("Ljung-Box Q")
        axes[2].legend()

        plt.tight_layout()
        plt.savefig("residual_diagnostics.png", dpi=300)
        plt.show()

Diagnostic Interpretation:

  • ACF Plots: Murphet's autocorrelation function shows fewer significant spikes, indicating the model has captured more of the data's structure.
  • Ljung-Box Test: The much lower Q statistic for Murphet means its residuals are closer to white noise, the ideal for time series models.
  • Impact on Forecasts: Better residual diagnostics translate to more reliable future forecasts, as the model has properly accounted for the data's patterns.
  • Practical Benefit: The improved diagnostics mean decision-makers can have higher confidence in Murphet's projections.

Implementation Tips

🔬

Model Selection

For bounded data like rates, conversions, or proportions, use likelihood="beta". For unbounded data, use likelihood="gaussian". The Beta head gives you the best results for anything in the (0,1) range.

⚡

Optimization Speed

Use inference="map" for rapid experimentation and hyperparameter search. Switch to inference="nuts" for your final model to get full Bayesian uncertainty estimates.

🔄

Seasonal Components

For most datasets, combining yearly periods=12.0 with quarterly periods=3.0 seasonality provides excellent results. Use auto_detect=True to automatically identify periods from your data.

Advanced Usage Guide